1_二進数を簡単にまとめると・・・
一言でまとめると、二進数は「数字を0と1の並びだけで表現する方法」です。
私たちがよく使用している表記方法は十進数と呼ばれ「数値を0から9までの値で表現する方法」
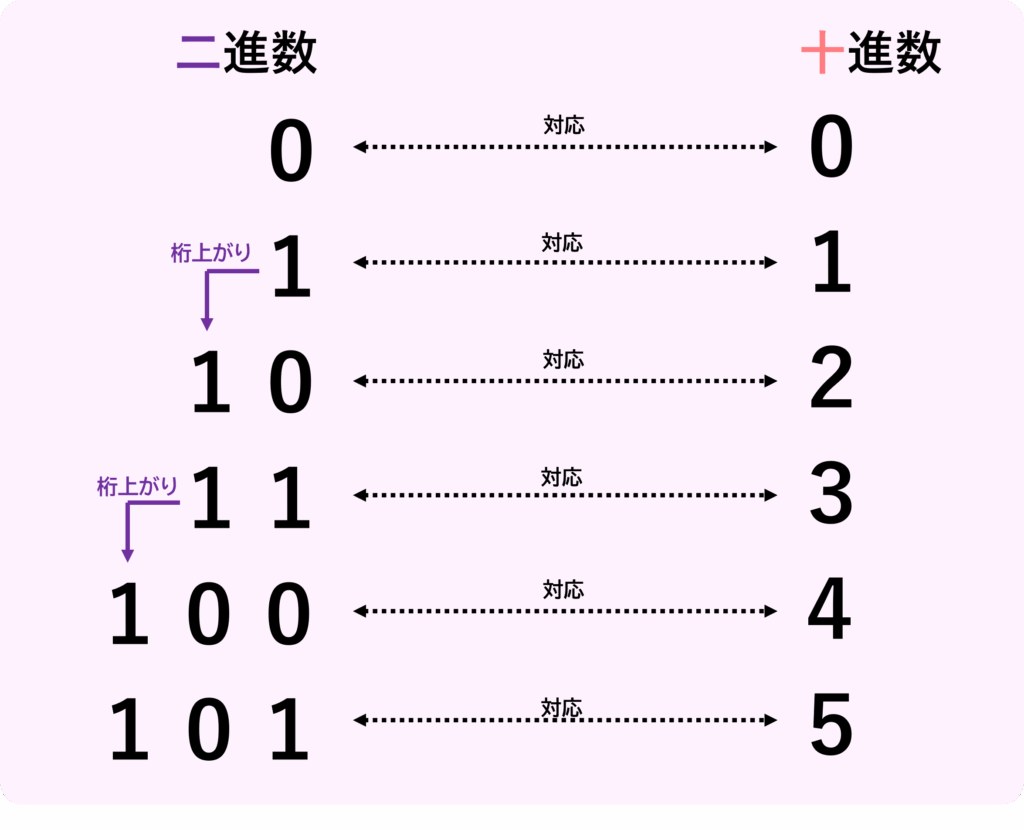
十進数の場合、0から始まり9を超えると桁上がりします(例:「9」→「10」)が、二進数に場合は、0から始まり1を超えると桁上がりします(例:「1」→「10」)。

バグ太郎
なぜ二進数のような考え方が必要なのですか?
なじみがない上に、1と0のみで表現している数値は逆に分かりにくい気が・・・

C-3PU
人間の方はそうなんでしょうね・・・ただ我々コンピュータが多くのデータを処理する時には、0と1のみで構成されていないと逆に理解できないんですよ・・・機械は電圧が高い・低いや、電源がON・OFFといった単純な2パターンを高速で処理する形式の方が効率がいいためです。
(難しく言うと、コンピュータ内部の物理特性に合っていて、もっともシンプルかつ高速・信頼性の高い情報表現方式)
2_図解化
二進数は、0と1のみで表現、十進数は、0から9の値で表現
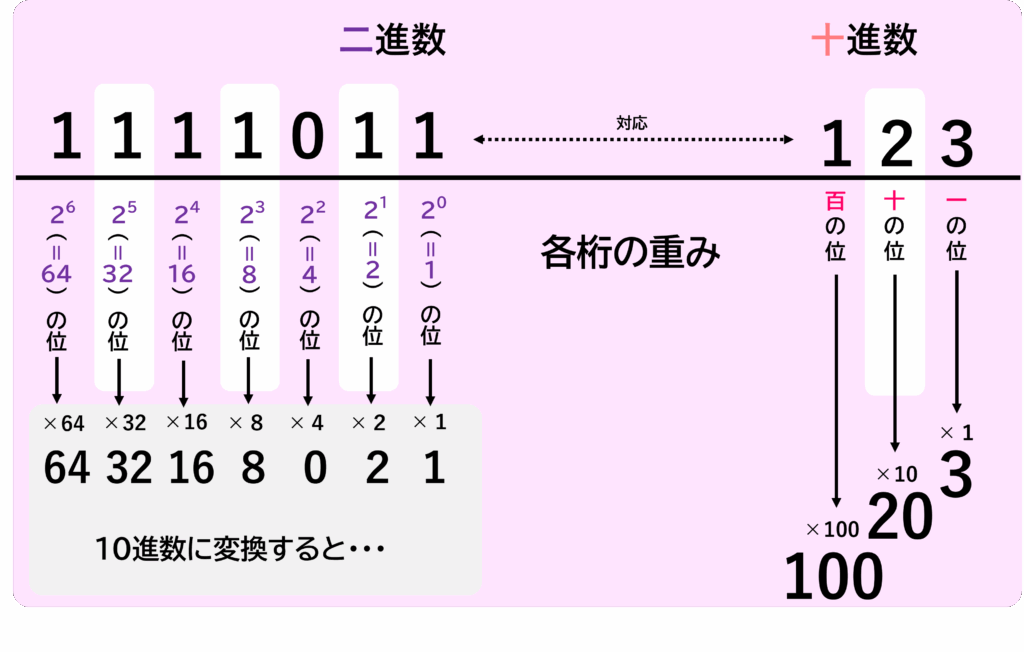
各桁の重みについて
10進数における「123」という数字について、各桁の値の重みが異なる(例:百の位の「1」、十の位の「2」では数字の重みが違います。実際は百の位の「1」は「100」であり、十の位の「2」は「20」である)ように、二進数についても各桁の重みが異なります。
3_二進数と十進数の変換
3-1_十進数から二進数への変換(2で割った余りを並べていく)

3-2_上記を繰り返してくき、2で割れなくなったら余りを下から並べていく
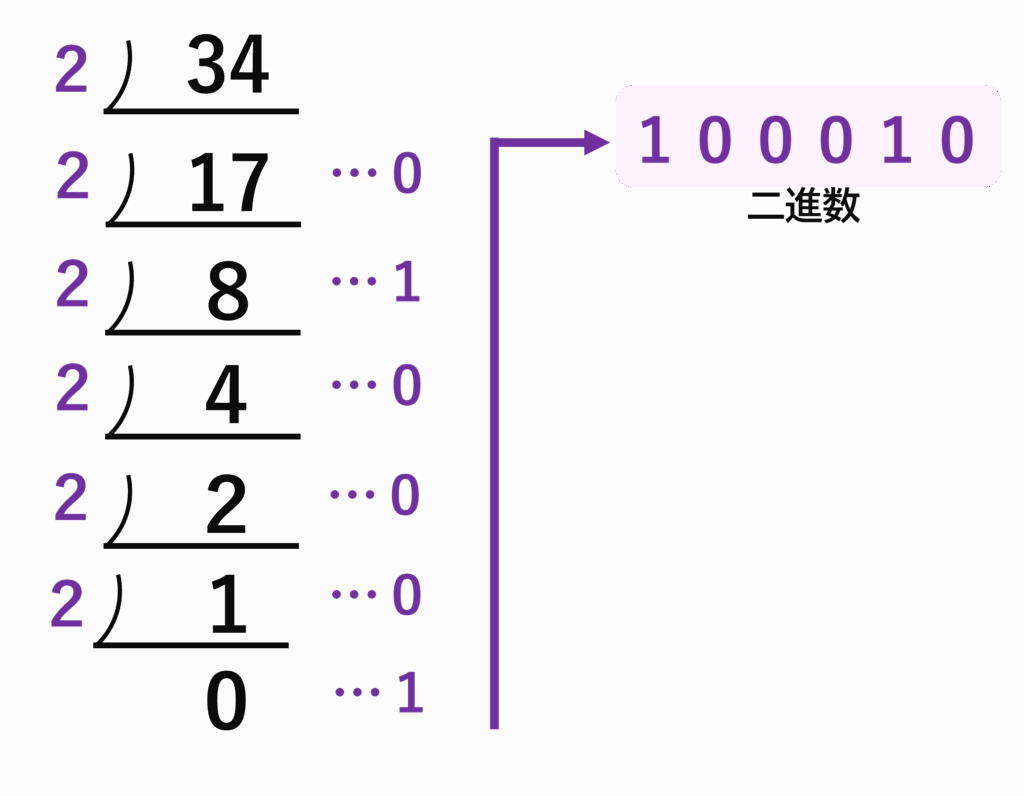

バグ太郎
このやり方でなんで二進数に変換できるのかがよく分かりません・・・

C-3PU
イメージとしては次のような例で考えてみるとよいです。十進数 123は「123 = 10×12 +3」と分解できるため、10で割ると3が余り、この3が一の位となります。同じように二進数変換なら「123 = 2×111 +1」と分解できるため、2で割ると1が余り、この1が二進数における2の0乗の位を表すと言えば、イメージが湧くでしょうか?

バグ太郎
ギリギリ・・・なんとか・・・
3-3_二進数を十進数へ変換(各桁の重みづけを掛けた上で、合計する)
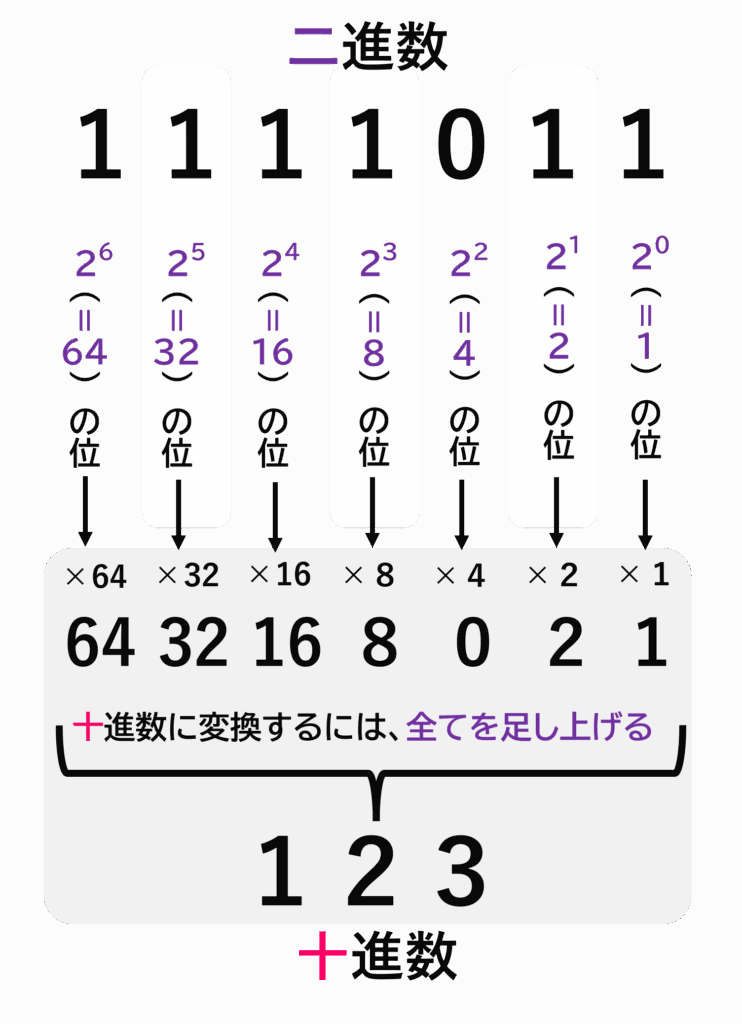



コメント